Homophily in Social Networks

Nowadays, social media is an essential part of people’s lives and as a result, the supply of social networks is booming. Such networked data are a great source for social network analytics since they represent our actual behavior on a massive scale. However, they differ from more traditional data sources since the relationships between the individuals play a role in a addition to the characteristics of the individuals themselves. Furthermore, in various network applications, there is correlation between the properties of adjacent nodes. Often, these properties are not distributed randomly in the network but are correlated with the underlying network structure. In social networks, this means that people tend to associate with others whom they perceive as being similar to themselves. The similarity can be e.g. age group, gender, origin, hobbies etc. This is known as homophily, a term used in sociology that can best be explained by the phrase: ‘Birds of a feather flock together.’

When individuals belong to one of two different groups, two parameters are needed to capture the interplay between the network structure and the underlying social network (Park and Barabási 2007). On one hand, the connectedness between nodes belonging to the different groups and on the other hand, connectedness between nodes belonging to the same group. These are concepts known as heterophilicity and dyadicity, respectively.

• Heterophilicity, measures the connectedness between nodes of different groups. In a heterophilic network, edges between nodes belonging to different groups are more common than in a random network and in a heterophobic network these edges are less common.
• Dyadicity measures the connectedness between nodes belonging to the same group. A network is dyadic if the nodes that belong to the same group are more connected amongst themselves than in a random network.

A network that is dyadic and heterophobic shows evidence of homophily.

How are heterophilicity and dyadicity measured in a social network?

Assume we have a group of ten data scientists that all have their preference for a specific technology. Some of them work mainly with R and the others perform all their analyses in Python. They therefore all belong to one of the two groups, R or Python. These scientists sometimes collaborate when they are working on data science problems. They can therefore be linked together to form a network. In this case, two data scientist are connected if they are currently working together. As a result we have three types of edges in the network, 1) edges that connect two R users, which we denote by ‘rr’, 2) edges that connect two Python users denoted by ‘pp’ and, 3) edges that connect an R user and a Python user, denoted by ‘rp’. The following commands are used to create this network in R.

library(igraph, quietly = TRUE, verbose = FALSE, warn.conflicts = FALSE)
names<-c('A','B','C','D','E','F','G','H','I','J')
tech<-c(rep('R',6), rep('P',4))
DataScientists<-data.frame(name=names, technology=tech)
DataScienceNetwork<-data.frame(from=c('A','A','A','A','B','B','C','C','D','D','D', 'E','F','F','G','G','H','H','I'),
    to=c('B','C','D','E','C','D','D','G','E','F', 'G','F','G','I','I','H','I','J','J'),
    label=c(rep('rr',7),'rp','rr','rr','rp','rr','rp','rp',rep('pp',5)))
g<-graph_from_data_frame(DataScienceNetwork, directed = FALSE)
V(g)$technology<-as.character(DataScientists$technology)

g
## IGRAPH UN-- 10 19 --
## + attr: name (v/c), technology (v/c), label (e/c)
## + edges (vertex names):
## [1] A--B A--C A--D A--E B--C B--D C--D C--G D--E D--F D--G E--F F--G F--I
## [15] G--I G--H H--I H--J I--J

The resulting network can be seen below. We colored the nodes depending on the preferred technology, where blue denotes R and green Python. We have also colored the edges depending on the color of the nodes they connect. Thus, blue edges connect two R nodes, green edges connect two Python nodes and the red edges connect an R and a Python node. These are the cross label edges. Clearly, R users tend to collaborate with each other and the same holds for the Python users. In contrast, there are not so many edges between the two groups.

This network of the data scientists and their preferred technology shows evidence of homophily.

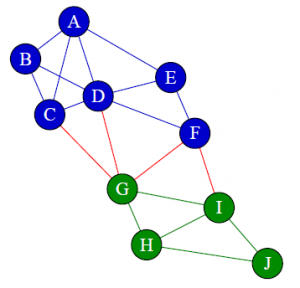
We can determine this by measuring the network’s heterophilicity and dyadicity, but first we compute some basic properties of the network. We need to know the number of nodes in the network and the number of nodes belonging to each group. These are the variables N, n_r and n_p in the code below. We also count the total number of edges, E, and the number of each type of edge, that is, edges connecting two R nodes, edges connecting two Python nodes and the cross label edges, represented by e_rr, e_pp and e_rp respectively.

#Number of nodes
N<-length(V(g))
n_r<-length(which(V(g)$technology=='R'))
n_p<-length(which(V(g)$technology=='P'))

#Number of edges
E<-length(E(g))
e_rr<-length(which(E(g)$label=='rr'))
e_pp<-length(which(E(g)$label=='pp'))
e_rp<-length(which(E(g)$label=='rp'))

In addition, we compute the connectedness of the network, which is the probability of two nodes being connected. It is obtained by dividing the actual number of edges, E, with the number of edges if the network was fully connected. The number of edges in a fully connected network of given by:

p<-2*E/N/(N-1)

We are now ready to compute the heterophilicity of the network, which is defined as the ratio between the actual number of cross label edges, e_rp, and the expected number of such edges in a random network.

bar_e_rp<-n_r*n_p*p
H<-e_rp/bar_e_rp
H

## [1] 0.3947368

In a similar way, we compute the dyadicity. Dyadicity is the ratio between the actual and the expected number of same label edges. Thus, it can be computed for each group separately. We denote the dyadicity for the R users and for the Python users by Dr and Dp. The following R commands show that both Dr and Dp are greater than 1, which mean that both groups are dyadic, i.e. there is more connectivity within the group of R users and within the group of Python users.

bar_e_rr<-n_r*(n_r-1)/2*p
D_r<-e_rr/bar_e_rr
D_r
## [1] 1.578947

bar_e_pp<-n_p*(n_p-1)/2*p
D_p<-e_pp/bar_e_pp
D_p
## [1] 1.973684

As a result, we can say that our network is homophilic in terms of their preferred technology! We have briefly demonstrated how to compute heterophilicity and dyadicity in a social network using R. Together they help determine whether a network shows signs of homophily and thus whether relationships between people play an important role in the network. This is important knowledge before applying social network analytics techniques such as featurization and network learning since they are more likely to be effective.

References

• Park, Juyong, and Albert-László Barabási. 2007. “Distribution of Node Characteristics in Complex Networks.”
  Proceedings of the National Academy of Sciences 104 (46). National Acad Sciences: 17916–20.