Contributed by: Eugen Stripling, Seppe vanden Broucke, Bart Baesens
This article first appeared in Data Science Briefings, the DataMiningApps newsletter. Subscribe now for free if you want to be the first to receive our feature articles, or follow us @DataMiningApps. Do you also wish to contribute to Data Science Briefings? Shoot us an e-mail over at briefings@dataminingapps.com and let’s get in touch!
Large online service providers such as Amazon, TripAdvisor, or Twitter have—soon or later—inevitably to cope with fraudulent activities on their platforms to remain trustworthy and reliable in the eye of the general public. On these platforms, fraudsters intentionally misrepresent facts and circumstances about themselves, their products, or their services to attain unjustified benefits that are created based on erroneous beliefs of honest users. To evade detection, fraudsters constantly adapt their strategies and strive to blend into the environment as best as possible [1]. One cunning way to disguise fraudulent behavior is to use “camouflage” in which smart fraudsters appear to look “normal” by also having connections to honest objects. The detection of such fraudulent user accounts on large platforms is a challenging task, even with the aid of analytical models.
Recently, Hooi et al. [2] proposed a state-of-the-art graph-based detection algorithm, called FRAUDAR, to effectively uncover camouflaged fraud accounts. In fact, they formally proved that there is an upper bound of connections a fraudster can have to avoid detections. In other words, their approach provides a theoretical guarantee that fraud will be detected if the fraudster’s number of connections exceeds the (data-dependent) threshold:
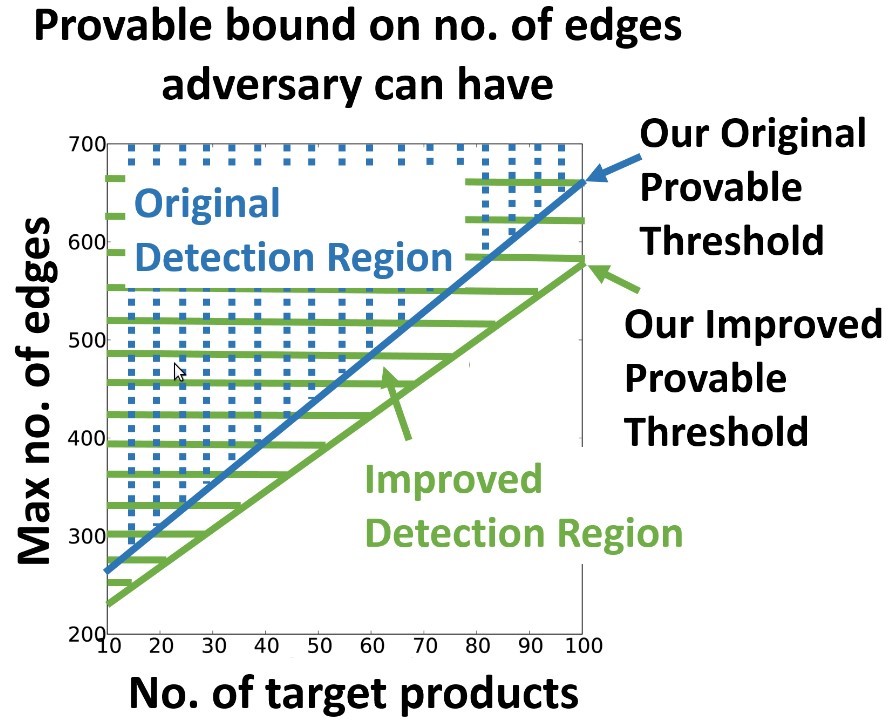
Figure 1: FRAUDAR’s theoretical bound on detectable region [2].
Furthermore, on a real-world Twitter graph with 41.7 million users and 1.47 billion followers, they showed that FRAUDAR spotted more than 4,000 fraudulent accounts that have not been previously detected by Twitter for seven years. The majority of the detected accounts showed clear signs of advertising follower-buying services (Figure 2).
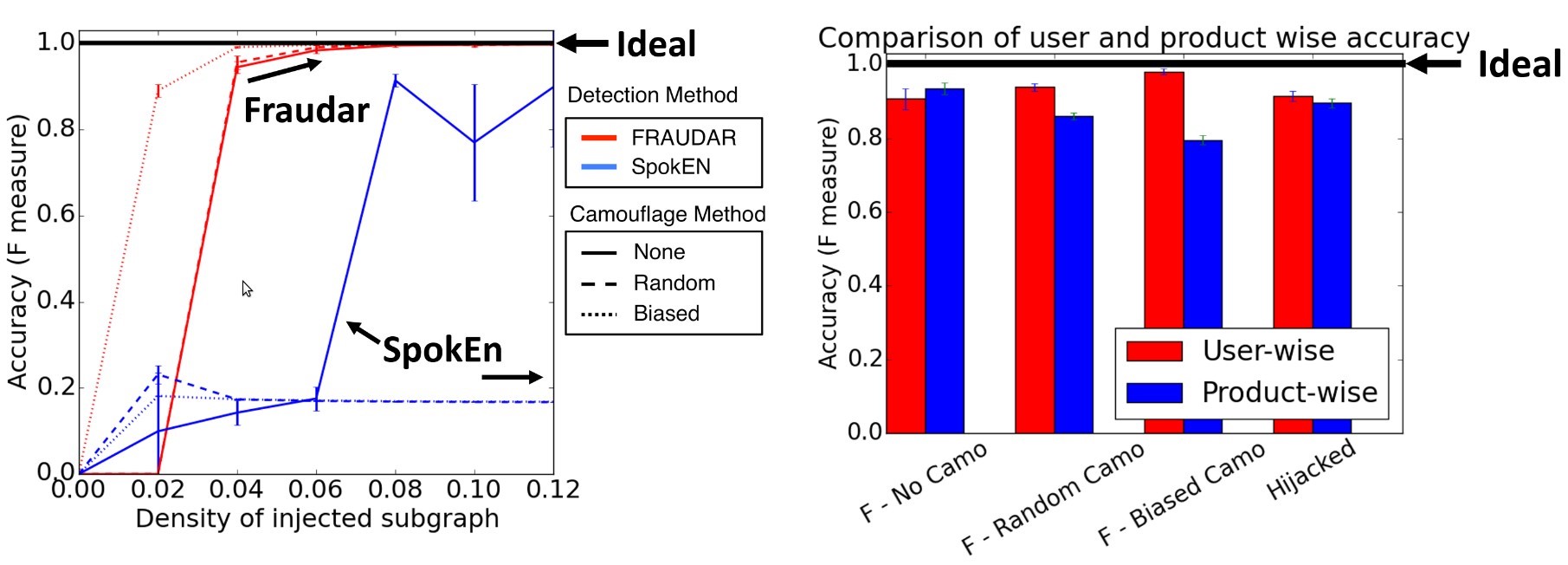
In a series of experiments, the authors tested FRAUDAR’s detection capabilities under various worst-case attack scenarios such as a number of different types of camouflaged fraudster accounts, as well as for the possibility of hijacked legitimate accounts (Figure 3). Two of the camouflage scenarios are: (1) random camouflage and (2) biased camouflage. In (1), fraudulent accounts randomly add connections to honest objects; whereas in (2), a scenario is simulated in which smart fraudsters deliberately add more connections to the popular honest objects to realistically appear like “normal” users.
Figure 2: Sample of a detected twitter account advertising a follower-buying service [2].
To detect fraudulent accounts under such challenging circumstances, FRAUDAR operates based on the assumption that people who take of advantage of follower-buying services such as TweepMe or TweeterGetter or buying top fake reviews for Amazon or TripAdvisor, have many connections between them and the hired fraudster accounts. A graph representation is thereby especially suitable for the description of the data. That is, consider a set of m users U = {u1,…,um} and n objects W = {w1,…,wn} connected via a bipartite graph G = (U ∪ W, E), where the set of edges, denoted E, only allows for connections between members of different sets. For example, on Amazon, the nodes or vertices of the graph, U and W, may represent user accounts and products, respectively. A review given by a user for a certain product establishes a connection or edge between them. By examining the graph for unexpectedly dense regions (e.g., a product has a suspiciously high amount of user reviews), FRAUDAR is able to detect the most suspicious subset of nodes by means of a camouflage-resistant density metric, which is also introduced by Hooi et al. [2].
Given a bipartite graph G = (U ∪ W, E), the FRAUDAR algorithm starts by computing the priorities of each node in the graph. Furthermore, let Xt denote the suspicious set at step t, which at the start is the entire set of nodes X0 = U ∪ W. Then, repeatedly remove the least suspicious node and update the priorities of its neighbors (priorities are closely connected to the density metric). That is, compute the density of the remaining graph without the node i under current consideration (i.e, Xt{i}), and remove the node that corresponds to the highest density value— leaving behind the most suspicious nodes. After running over all nodes, FRAUDAR returns the set Xt, t = 0,…,m + n, with the highest density. The optimal suspicious set holds the block of nodes with a suspiciously dense connectivity, and can now be targeted for investigation. Choosing an appropriate data structure (i.e., a so-called priority tree), the algorithm runs in near-linear time with complexity O(|E|log|V|), |V| being the number of vertices in the graph (Figure 4). Obviously, the key component of the algorithm is to measure density. Hooi et al. [2] introduced a novel family of metrics with intuitive axioms that provides several advantages as a suspiciousness metric. Ultimately, this class of metrics allows proving formally that the density metric is camouflage-resistance and offers theoretical guarantees for the detection of fraud. For more technical information about the density metric, we refer the interested reader to the paper.

Figure 3: Three examples of possible attacks investigated in the experiments [2].
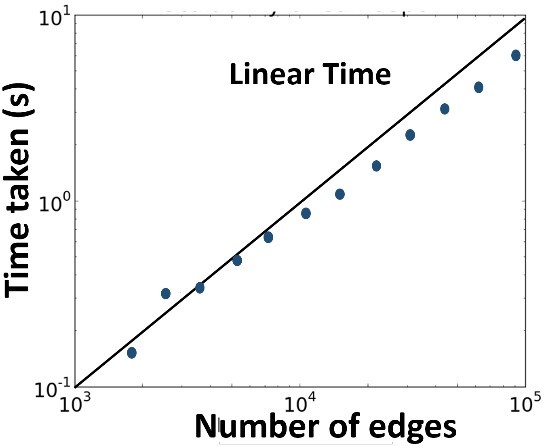
Figure 4: FRAUDAR runs in near-linear time [2].
The authors tested their fraud detection algorithm under various camouflage settings (relate to Figure 3). Despite the challenging conditions, they were able to show that FRAUDAR outperforms the competitor and detects fraudulent users as well as fraudulent objects with high accuracy (Figure 5). Moreover, in a controlled experiment, they showed that FRAUDAR is very effective in detecting fraudulent user accounts in the real-world Twitter graph with millions of nodes and billions of edges (Figure 6).
Figure 5: FRAUDAR outperforms the competitive algorithm in various camouflage scenarios [2] (links to larger version).
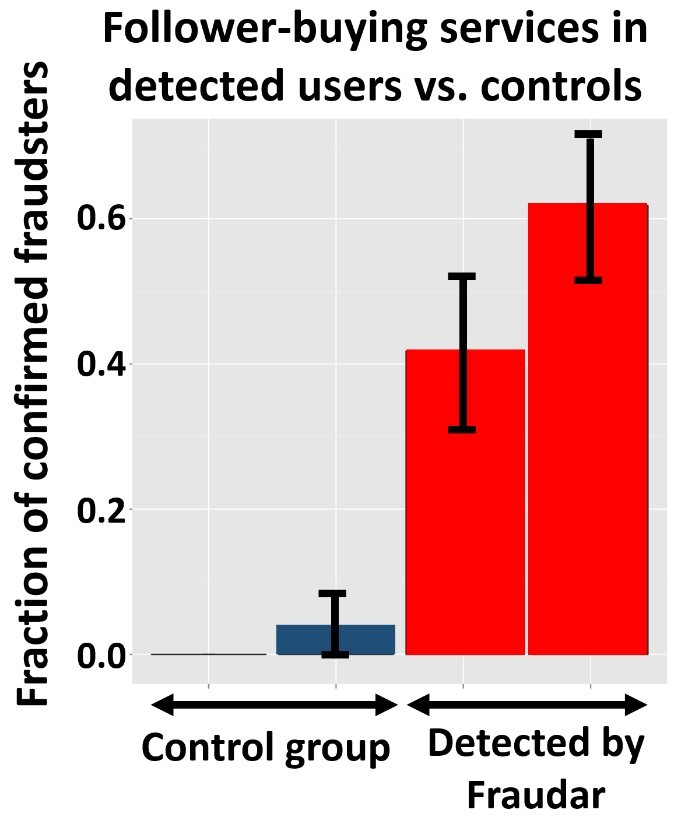
Figure 6: FRAUDAR is able to detect many confirmed fraudsters in real-world Twitter data [2].
Given the amount of research contributions, as well as their practical relevance and application, it is not surprising that this paper won the Best Paper Award (Research track) of the 22nd ACM SIGKDD Conference on Knowledge Discovery and Data Mining.[footnote 1]
References
- [1] Baesens, V. V. Vlasselaer, and W. Verbeke, Fraud Analytics Using Descriptive, Predictive, and Social Network Techniques: A Guide to Data Science for Fraud Detection, 1st ed. Wiley Publishing, 2015.
- [2] Hooi, H. A. Song, A. Beutel, N. Shah, K. Shin, and C. Faloutsos, “FRAUDAR: Bounding Graph Fraud in the Face of Camouflage,” in Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, August 13-17, 2016, 2016, pp. 895–904. [Online]. Available: http://doi.acm.org/10.1145/2939672.2939747
- [Footnote 1] http://www.kdd.org/awards/view/2016-sigkdd-best-paper-award-winners