By: Bart Baesens, Seppe vanden Broucke
This QA first appeared in Data Science Briefings, the DataMiningApps newsletter as a “Free Tweet Consulting Experience” — where we answer a data science or analytics question of 140 characters maximum. Also want to submit your question? Just Tweet us @DataMiningApps. Want to remain anonymous? Then send us a direct message and we’ll keep all your details private. Subscribe now for free if you want to be the first to receive our articles and stay up to data on data science news, or follow us @DataMiningApps.
You asked: What is SMOTE in an imbalanced class setting (e.g. fraud detection)?
Our answer:
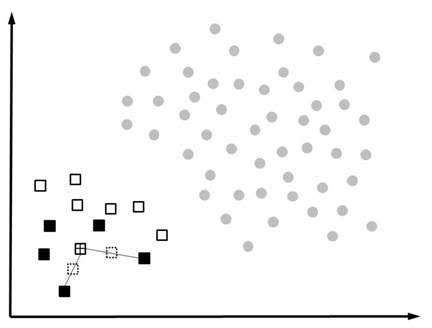
Rather than replicating the minority observations (e.g., defaulters, fraudsters, churners), Synthetic Minority Oversampling (SMOTE) works by creating synthetic observations based upon the existing minority observations (Chawla et al., 2002). This is illustrated in the below figure where the circles represent the majority class (e.g. non-defaulters) and the squares the minority class (e.g. defaulters). For each minority class observation, SMOTE calculates the k nearest neighbors. Let’s assume we consider the crossed square and pick the 5 nearest neighbors represented by the black squares. Depending upon the amount of oversampling needed, one or more of the k-nearest neighbors are selected to create the synthetic examples. Let’s say our oversampling percentage is set at 200%. In this case, 2 of the 5 nearest neighbors are selected at random. The next step is then to randomly create two synthetic examples along the line connecting the observation under investigation (crossed square) with the two random nearest neighbors. These 2 synthetic examples are represented by dashed squares in the figure.
As an example, consider an observation with characteristics (e.g. age and income) of 30 and 1000, and its nearest neighbor with corresponding characteristics 62 and 3200. We generate a random number between 0 and 1, let’s say 0.75. The synthetic example then has age 30+0,75*(62-30) or 54, and income 1000+0,75*(3200-1000)=2650. SMOTE then combines the synthetic oversampling of the minority class with undersampling the majority class. Note that in their original paper, Chawla et al (2001) also developed an extension of SMOTE to work with categorical variables. Empirical evidence has shown that SMOTE usually works better than either under- or oversampling. Also for fraud detection it has proven to be very valuable.