By: Bart Baesens, Seppe vanden Broucke
This QA first appeared in Data Science Briefings, the DataMiningApps newsletter as a “Free Tweet Consulting Experience” — where we answer a data science or analytics question of 140 characters maximum. Also want to submit your question? Just Tweet us @DataMiningApps. Want to remain anonymous? Then send us a direct message and we’ll keep all your details private. Subscribe now for free if you want to be the first to receive our articles and stay up to data on data science news, or follow us @DataMiningApps.
You asked: How can you interpret the coefficients of a logistic regression model?
Our answer:
Logistic regression estimates the following model:
![]() ,
,
where Y corresponds to fraud, default, churn, response, etc. and X1, …XN are the predictors (e.g. age, income, etc.). This can be reformulated in terms of the odds as follows:
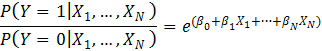
The log(odds) or logit then becomes:
![]()
To interpret a logistic regression model, one can calculate the odds ratio. Suppose variable Xi (e.g. age, income, etc.) increases with one unit with all other variables being kept constant (ceteris paribus), then the new logit becomes the old logit with βi added. Likewise, the new odds become the old odds multiplied by eβi. The latter represents the odds ratio, i.e. the multiplicative increase in the odds when Xi increases by 1 (ceteris paribus). Hence,
- βi > 0 implies eβi > 1 and the odds and probability increase with Xi
- βi < 0 implies eβi < 1 and the odds and probability decrease with Xi
Another way of interpreting a logistic regression model is by calculating the doubling amount. This represents the amount of change required for doubling the primary outcome odds. It can be easily seen that for a particular variable Xi, the doubling amount equals log(2)/βi.
