By: Bart Baesens, Seppe vanden Broucke
This QA first appeared in Data Science Briefings, the DataMiningApps newsletter as a “Free Tweet Consulting Experience” — where we answer a data science or analytics question of 140 characters maximum. Also want to submit your question? Just Tweet us @DataMiningApps. Want to remain anonymous? Then send us a direct message and we’ll keep all your details private. Subscribe now for free if you want to be the first to receive our articles and stay up to data on data science news, or follow us @DataMiningApps.
You asked: How do you evaluate random forests?
Our answer:
Various benchmarking studies have shown that random forests can achieve excellent predictive performance. Actually, they generally rank amongst the best performing models across a wide variety of prediction tasks. They are also perfectly capable of dealing with data sets that only have a few observations, but lots of variables. They are highly recommended when high performing analytical methods are needed. However, the price that is paid for this is that they are essentially black box models. Due to the multitude of decision trees that make up the ensemble, it is very hard to see how the final classification is made. One way to shed some light on the internal workings of an ensemble is by calculating the variable importance. A popular procedure to do so is as follows:
- Permute the values of the variable under consideration (e.g. x[j]) on the validation or test set.
- For each tree, calculate the difference between the error on the original, unpermutated data and the error on the data with x[j] permutated as follows:
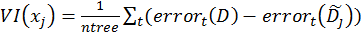where ntree represents the number of trees in the ensemble, D the original data, and ~D[J] the data with variable x[j] permutated. In a regression setting, the error can be the mean squared error (MSE), whereas in a classification setting, the error can be the misclassification rate. - Order all variables according to their VI value. The variable with the highest VI value is the most important one.
