Deep Learning for Credit Scoring

Introduction

The development of quantitative credit scoring models that accurately distinguish defaulters from non-defaulters has become a major focus of financial institutions today. Therefore, the performance of different classification algorithms for credit scoring has been heavily researched over the past decades. Logistic regression is the most successful of these methods but decision trees have also found favour. These two methods can be seen as being examples of conventional methods for credit scoring. More recently, research on classification algorithms for credit scoring has taken account of the development of ensemble methods. One such method, random forest, has been particularly successful and can be considered as a benchmark method for credit scoring. However, another development in machine learning, that is the development of large scale neural networks, i.e. deep learning, has received little attention in the credit scoring community which underlines the main contribution of this project. Novel deep learning architectures were constructed and their performance compared to the performance of both the benchmark method and conventional methods for credit scoring.

Methods

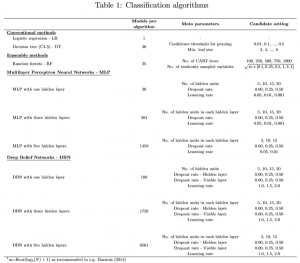
The different classifiers considered here and the tuning grid for their meta parameters are given in table 1 (click to enlarge).

A logistic regression model estimates a probability of a borrower defaulting on a loan by using the logistic function. Decision trees however are recursive partitioning algorithms that come up with a tree like structure representing patterns in the data with the aim of partitioning the data into groups that are as homogeneous as possible in terms of the variable to be predicted. Ensemble models estimate multiple analytical models instead of using only one model. Random forests is one such method that creates an ensemble, a forest, of decision trees during training and then the forest outputs the class that the majority of the trees predict. Key in this approach is that each tree in the forest sees a random bootstrap sample of the data and also that a selection of a random subset of attributes is carried out at each node. Therefore the trees will differ and the ensemble will be superior in performance then its base classifiers. Two deep learning algorithms, a multilayer perceptron network (MLP) and a deep belief network (DBN), were also considered. A relu activation function was used in the hidden layers of the MLP network and a softmax function with two neurons was used in the output layer of that network. This network has no inherent ability to solve complex function since its weights are initialized randomly. But then each layer is allowed to propagate their activation to forward layers and iteratively fix their weights during backpropagation which aims at minimizing the difference between the actual output vector of the network and the desired output vector. Here rmsprop backpropagation was used to speed up gradient descent. A DBN is a constructed by using several layers of restricted Boltzmann machines (RBM). An RBM is a bipartite graph in which visible units represent observations which are connected to units in a hidden layer which learn to represent features using weight connections. The DBN aims at maximizing the likelihood of the training data, therefore the training process starts at the lowest level RBM were visible layer is the input vector. Then the training progressively moves up until finally the RBM, containing the outputs of the DBN, is trained. By doing this sequence of operation one obtains a unbiased sample of the kind of vectors of visible values (inputs) the network believes in. This training process is unsupervised but can easily be turned into a classification model by adding a additional layer to the model which simply tunes the existing feature detectors that were discovered during unsupervised training using backpropagation. Dropout was used when training both the MLP and DBN models to prevent overfitting.

All models considered in this comparison, except logistic regression, exhibit meta-parameters that need to be specified by the user. Both the MLP and the DBN networks were constructed using one, three and five hidden layers. The number of models that one needs to consider for these networks grows exponentially with the number of hidden layers used. Constructing these models is a computationally expensive task that often requires training many networks with different configuration to obtain a good solution which can be seen as a drawback of these models.

Results

The classifiers were compared over three data sets and four performance measures; the AUC, The Brier score, the partial-Gini and the EMP measure. Two main conclusions emerge from this comparison. Firstly, random forests is the overall best performing classifier over all data sets and performance indicators. Furthermore the classifier performs statistically significantly better then all other classifiers considered, except logistic regression. Secondly, deep networks with a number of hidden layers do not perform better then shallower networks with one hidden layer in general. It should also be taken into account in this comparison that the deep networks come with much greater computational cost then other classifiers considered here since the number of models that one needs to construct to adequately tune the meta parameters of the models grows exponentially with the number of hidden layers. Deep learning has been successfully applied to a number of different fields and has turned out to be very good at discovering intricate structures in high-dimensional data. However, the data sets used here, and in credit scoring in general, would not be considered to be very highly-dimensional. This could be seen as a possible reason why the deeper networks don’t provide considerable improvements on the performance of their shallower counterparts. From the above one can conclude that deep learning algorithms do not seem to be appropriate models for credit scoring and that random forests should continue to be considered as a benchmark method for credit scoring.

References

• Baesens, B. (2014). Analytics in a big data world: The essential guide to data science and its applications. John Wiley & Sons.
• Breiman, L. (2001). Random forests. Machine learning, 45(1):5–32.
• Hinton, G. (2012). rmsprop: Divide the gradient by a running average of its recent magnitude. https://www.coursera.org/learn/neural-networks/lecture/YQHki/ rmsprop-divide-the-gradient-by-a-running-average-of-its-recent-magnitude. Online: Accessed 23.April 2018.
• Hinton, G. E. (2007). Boltzmann machine. Scholarpedia, 2(5):1668. revision #91075.
• Hinton, G. E. (2009). Deep belief networks. Scholarpedia, 4(5):5947. revision #91189.
• Lopes, N. and Ribeiro, B. (2015). Machine Learning for Adaptive Many-Core Machines-A Practical Approach. Springer.
• Luo, C., Wu, D., and Wu, D. (2017). A deep learning approach for credit scoring using credit default swaps. Engineering Applications of Artificial Intelligence, 65:465–470.
• Mohamed, A.-r., Dahl, G. E., and Hinton, G. (2012). Acoustic modeling using deep belief networks. IEEE Transactions on Audio, Speech, and Language Processing, 20(1):14–22.
• Spanoudes, P. and Nguyen, T. (2017). Deep learning in customer churn prediction: Unsupervised feature learning on abstract company independent feature vectors. arXiv preprint arXiv:1703.03869.

Do you also wish to contribute to Data Science Briefings? Shoot us an e-mail (just reply to this one) and let’s get in touch!