This article first appeared in Data Science Briefings, the DataMiningApps newsletter. Subscribe now for free if you want to be the first to receive our feature articles, or follow us @DataMiningApps. Do you also wish to contribute to Data Science Briefings? Shoot us an e-mail over at briefings@dataminingapps.com and let’s get in touch!
Contributed by: Seppe vanden Broucke and Bart Baesens. This article was adopted from our Managing Model Risk book. Check out managingmodelriskbook.com to learn more.
Data is the key ingredient to any analytical model, and no analytical model can be built without it. However, it is a pipe dream to believe data is always perfect and comes without risk. Moreover, since it directly feeds into the analytical model construction, it can affect multiple and various analytical models simultaneously since the they often rely upon common data sources. An an example, many companies will use the features “age” and “employment status” of a customer to predict churn, fraud, credit and/or response to marketing campaigns.
In this article we explore the issue of data bias and discuss the different origins of data bias. To kick off, let’s briefly discuss an example of survival bias. The famous statistician Abraham Wald (known for the Wald Chi-Squared test) analyzed how to minimize bomber plane losses due to enemy fire in World War II. He started by analyzing bomber damage by using a sample of bombers that returned home from their mission. You can see an example in the figure below (taken from Wikipedia), with the dots representing the damage on a bomber that successfully made it back home:
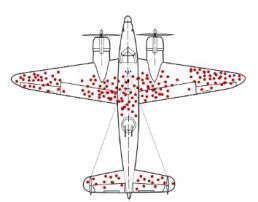
The question, then, was where armor should be added to maximize a bomber’s survival chances? Obviously, not to the dotted parts, as the sample returning is a biased sample since these represent the ones that survived. The bombers that didn’t make it probably got hit at other places and it were exactly these intact places that should be further reinforced. This clearly indicates that depending upon the setting, the concept of bias needs careful thought and is not necessarily an impassable obstacle to develop a successful strategy.
Data bias is a perennial problem in any analytics setting. Actually, it was David Hand who, in a credit scoring context stated that as soon as a scorecard gets implemented, it is outdated. This idea also applies to other settings such as fraud detection, marketing analytics, etc. It is unfortunately a reality that us data scientists have to learn to live with, but which is not necessarily a showstopper for the success of analytics.
Let’s zoom into somewhat more detail. An analytics model is built on a sample of data which was collected during a specific time span. Hence, it is conditional on both the internal and external situation during this very specific time period. More specifically, during this period, exogenous events may have taken place such as a macro-economic upturn or downturn. Such exogenous events will obviously have an effect on the data collected and can lead to a first origin of data bias.
A second origin of data bias relates to the strategy of the party developing the model, such as a company, was adopting during the period of data collection. Examples of strategies are investing in customer retention, acquisition, a combination of both, a merger or acquisition, introducing a new product or service, etc. Let’s look at a specific example of this using a credit risk context. Before using any analytics for credit risk modeling, banks were using credit acceptance policies based on expert intuition or common sense which were assembled during many years of business experience. For example, it is quite obvious that a customer who is currently unemployed and has a substantial amount of accumulated debt, should not be given credit. Once the bank has decided to invest in analytics to automate its credit decisions, it can only start from a prefiltered or in other words biased data sample, since this sample will never contain unemployed customers with big accumulated debt. Since the analytical model has never seen this type of customers, it will not know that they should be considered as bad payers. This is the so called reject inference problem in credit scoring which essentially boils down to a data bias problem. Several solutions have been developed for this with the best option being to gather external data (e.g. from credit bureaus) about these customers who were denied credit in the past
A third origin of data bias concerns the endogenous traits of the instances in the model development sample such as changed sociodemographic behavior, continuously evolving interest in old and new products, etc. As an example, marital status used to be an important discriminator for credit scoring, but due to the fact that people are less likely to marry nowadays, it might make less sense to consider this.
These three sources of data bias will obviously change as the analytical model gets put into production. This problem is further exacerbated because of the time lag between the model development sample and the population on which the model will actually be used. However, this need not be a problem depending upon whether the analytical model is meant to be used for discrimination or calibration. Discrimination refers to what extent the model manages to distinguish between groups of instances (e.g. churners versus non-churners, high CLV customers versus low CLV customers, fraudsters versus non-fraudsters, bad payers versus good payers). In other words, discrimination refers to ranking instances in terms of the target variable under study and as such focuses on the ordinal aspect of the model. Calibration refers to the extent to which the actual value predicted by the model (e.g. predicted sales, predicted probability of default) is in line with what is actually observed in reality or in other words the cardinal aspect of the target variable under study.
What we have often seen in reality is that exogenous shocks (e.g., a macro-economicindex{economy} crisis, or the outbreak of a pandemic), do not impact the model discrimination primarily, but especially the model calibration. The e.g. most likely churners will remain the most likely churners but their churn probability might have increased. Hence, a complete model re-estimation is not necessarily needed, though its calibrated output should be tweaked using a well-determined scaling factor. The latter can then be determined using either expert input or a small tuning sample consisting of before and after observations. Endogenous changes in the customer population or changes in company strategy on the other hand are much more invasive. These usually imply a radical change in customer characteristics such that both the model discrimination and model calibration will suffer and a complete re-estimation of the analytical model is most likely needed. In highly volatile settings, it is recommended to cater for an ICT architecture that can easily re-estimate analytical models whenever desirable and deploy them into production (though this comes with its own validation challenges).
